domingo, 21 de agosto de 2011

calculo diferencial

El Cálculo Diferencial, es una parte importante del análisis matemático y dentro del mismo del cálculo infinitesimal Consiste en el estudio del cambio de las variables dependientes cuando cambian las variables independientes de las funciones o campos objetos del análisis. El principal objeto de estudio en el cálculo diferencial es la derivada. Una noción estrechamente relacionada es la de diferencial.
En el estudio del cambio de una función cuando cambian sus variables independientes es de especial interés para el cálculo diferencial el caso en el que el cambio de las variables es infinitesimal, esto es, cuando dicho cambio tiende a cero (se hace tan pequeño como se desee). Y es que el cálculo diferencial se apoya constantemente en el concepto básico del límite. El paso al límite es la principal herramienta que permite desarrollar la teoría del cálculo diferencial y la que lo diferencia claramente del álgebra.
Desde el punto de vista matemático de las funciones y la geometría, la derivada de una función en un cierto punto es una medida de la tasa en la cual una función cambia conforme un argumento se modifica. Esto es, una derivada involucra, en términos matemáticos, una tasa de cambio. Una derivada es el cálculo de las pendientes instantáneas de f(x) en cada punto x. Esto se corresponde a las pendientes de las tangentes de la gráfica de dicha función en sus puntos (una tangente por punto); Las derivadas pueden ser utilizadas para conocer la concavidad de una función, sus intervalos de crecimiento, sus máximos y mínimos.
Publicado por en No hay comentarios:

Derivadas y la relatividad

uno de los conceptos esenciales sobre el que gira toda la teoría de la relatividad general es el de derivada covariante (a veces impropiamente llamada conexión afín), que fue definida por primera vez por el matemático italiano Tullio Levi-Civita y que puede ser considerada tanto desde una perspectiva física como desde otra matemática. Desde un punto de vista físico, la derivada ordinaria de la velocidad es la aceleración de un cuerpo medida por un observador externo en reposo respecto a un campo gravitatorio (por ejemplo, un astrónomo situado sobre la superficie terrestre). En este caso el observador se mantiene a una distancia r constante del centro de masas, pero no así el objeto observado, que progresivamente se va aproximando al origen del campo gravitatorio.
Por el contrario, la derivada covariante de la velocidad \left(\frac{D \vec u}{d\tau}\right) es la aceleración medida por un observador comóvil, es decir, que está en reposo respecto al cuerpo en caída libre (por ejemplo, el piloto de un avión en caída libre o los tripulantes de una nave espacial con sus motores apagados).
En resumidas cuentas, la derivada ordinaria se utiliza para computar la aceleración ordinaria de un cuerpo, mientras que la derivada covariante es empleada para calcular su aceleración inercial. Según la mecánica galileana y newtoniana estos dos tipos de aceleración son idénticos, y en base a este axioma se desarrollaron nuevos principios mecánicos como el Principio de d'Alembert. Sin embargo, del principio de equivalencia de Einstein se deduce que cuando un cuerpo está sometido a un campo gravitatorio, su aceleración ordinaria cambia, pero no su aceleración inercial. De ahí que para Einstein fuera absolutamente necesario introducir en su teoría el concepto de derivada covariante.
Publicado por en No hay comentarios:

limite inferior y superior


Límite deExpresión
Una constante \lim_{x \to c} k =\, k\,
La función identidad \lim_{x \to c} x = \, c \,
El producto de una función y una constante \lim_{x \to c} kf(x) =\, k\lim_{x \to c} f(x)\,
Una suma \lim_{x \to c} (f(x) + g(x)) =\, \lim_{x \to c} f(x) + \lim_{x \to c} g(x)\,
Una resta \lim_{x \to c} (f(x) - g(x)) =\, \lim_{x \to c} f(x) - \lim_{x \to c} g(x)\,
Un producto 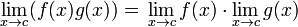\lim_{x \to c} (f(x) g(x)) =\, \lim_{x \to c} f(x) \cdot \lim_{x \to c} g(x)\,
Un cociente \lim_{x \to c} {{f(x)}\over {g(x)}} =\, {{\lim_{x \to c} {f(x)}} \over {\lim_{x \to c} {g(x)}}}\,\ \mbox{si } \lim_{x \to c} g(x) \ne 0,
Una potencia {\lim_{x \to c} f(x)^{g(x)}} =\, {\lim_{x \to c} f(x)^{\lim_{x \to c} g(x)}}\,\ \mbox{si } f(x) > 0
Un logaritmo {\lim_{x \to c} \log f(x)} =\, \log {\lim_{x \to c} f(x)}
El número e {\lim_{x \to 0} \left(1+x\right)^{1 \over x}} =\, {\lim_{x \to \infty} \left(1+{1 \over x}\right)^x } =\, e
Función f(x) acotada y g(x) infinitesimal {\lim_{x \to c} \left(f(x) \cdot g(x)\right)} =\, 0

En matemáticas se define límite superior y límite inferior de una sucesión (xn) como el mayor y menor límite convergente de las subsecuencias de (xn). Análogamente a éste, el límite superior y límite inferior para funciones reales se define de la misma manera.nferior. El límite superior y el límite inferior son un sustituto parcial para el límite, si es que éste no existe.

 Definición formal

Formalmente el límite inferior de una sucesión (xn) se define como
\sup_{n\geq 0}\,\inf_{k\geq n}x_k=\sup\{\inf\{x_k:k\geq n\}:n\geq 0\}
o también como
\lim_{n\rightarrow\infty}\left(\inf_{k\geq n}x_k\right)
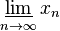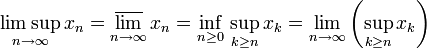y se denota como \liminf_{n\rightarrow\infty}x_n o como \varliminf_{n\rightarrow\infty}x_n. Análogamente se define \limsup_{n\rightarrow\infty}x_n=\varlimsup_{n\rightarrow\infty}x_n=\inf_{n\geq 0}\,\sup_{k\geq n}x_k=\lim_{n\rightarrow\infty}\left(\sup_{k\geq n}x_k\right).
Estas definiciones son útiles en un conjunto parcialmente ordenado en un sentido cuantitativo, y proporcionan que el supremo y el ínfimo existan. En una red reticular completa siempre existen estos valores, por lo que en este caso, cada secuencia tiene un límite inferior y límite superior asociado.
Si existe el límite inferior y el límite superior de una sucesión (xn), se cumple que \liminf_{n\rightarrow\infty}x_n\leq\limsup_{n\rightarrow\infty}x_n\;.
Publicado por en 1 comentario:
Suscribirse a: Entradas (Atom)